Formal Models
Language
- "T" is some alphabet for some set of languages {e.g., character
set for machine}
- T* is all possible sequences: "strings", "words" or "tokens" that
can be formed from the alphabet
- a "language" is some sub-set of T*
- a Language is a 4-tuple:
L(T, N, P, S) T = terminals N =
non-terminals P = production rules S = start sym.
In other words, a language is defined by a grammar.
Classes of Grammars
In 1950 Noam
Chomsky (a noted Linguist) described four classes of languages (in
order of increasing power).
- Type 3 - Regular languages (lex)
- Type 2 - Context free - Backus-Naur Form (yacc)
- restricted to rules of the form: A - > cBdE
(i.e., a non-terminal must appear singularily on the LHS of any
production rule, and the RHS side can be any
string of terminals and non-terminals).
- The non-terminal can be replaced by its RHS regardless of the
context it appears in.
- Type 1 - Context sensitive
restricted to rules of the form: a - > b where |a| < |b| (i.e., a and b
can be any string of terminals and non-terminals but b must be the
same length or longer than a)
- Type 0 - Unrestricted, recursively enumerable, phrase structure
- restricted to rules of the form: a -> b where a and b can be any
string of terminal and non-terminals
Type 0 and type 1 are important in theoretical computer
science, but have little impact on programming language design.
This collection of different types of Chomsky grammars is often referred
to as the Chomsky hierarchy. What do we mean by this and is it true?
We interpret this to mean that all type 3 languages are also type 2
languages and that all type 2 languages are also type 1 and all type 1
are also type 0.
Type3  Type2
Type2  Type1
Type1
 Type0
Type0
Remember that all the Chomsky grammars are characterised by their productions
which take the form:
X -> Y
The differences lie in what is permitted for X and Y.
Summary of Chomsky grammars
| Language Type |
X |
Y |
|
0
|
Any non-empty sequence of terminals and non-terminals |
Any sequence of terminals and non-terminals |
|
1
|
As type 0 |
As type 0 but must be longer than X
(this means that it cannot be empty) |
|
2
|
A single non-terminal |
Any sequence of terminals and non-terminals |
|
3
|
A single non-terminal |
A single terminal
Empty
A single terminal followed by a single non-terminal |
Formal Machine Models
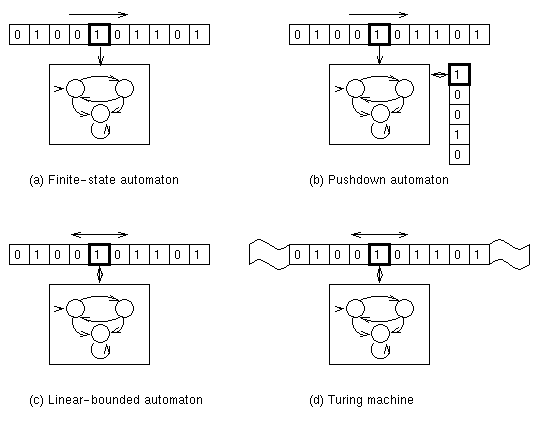
Finite State Automaton (FSA)
A graph with directed labeled arcs, two types of nodes
(final and non-final state), and a unique start state is an FSA:
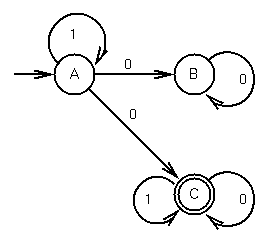
What strings start in state A and end up at state C?
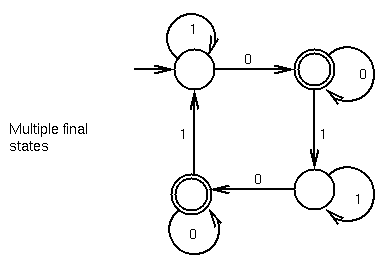
FSA's can have more than one final state:
Non-deterministic FSA vs. Deterministic FSA
- Deterministic FSA - For each state and for
each member of the alphabet, there is exactly one transition
- Non-deterministic FSA (NFA) - Remove above restriction.
At each node there is 0, 1 or more than one transition for each alphabet
symbol.
- Important early result: NFA = DFA
Outline of a Proof
Let subsets of states be states in DFA. Keep track
of which subset you can be in.
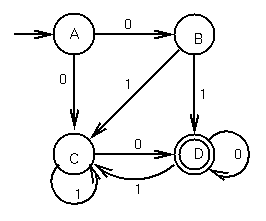
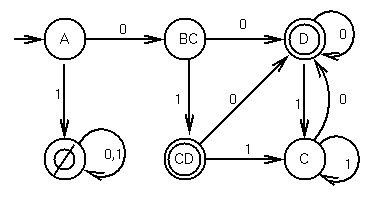
Any string from {A} to either {D} or {CD} represents a
path from A to D in the original NFA.
Regular Expressions
You can write any regular language as a regular expression:
0*11*1 + 0*11*(0 + 100*1)1*
The operators used in forming regular expressions are:
- Concatenation (adjacency)
- Or ( + sometimes written as | )
- Kleene closure (* -- 0 or more instances)
- also parenthesis for grouping
How would we write a regular expression for strings that contain at
least two a's? Note that it is not necessary that the two a's be
contiguous. One such regular expression is (a+b)*a(a+b)*a(a+b)*.
Another is b*ab*a(a+b)*. The difference in these two regular
expressions becomes obvious when you attempt to generate a
particular string using the regular expression. How would you
generate babaaba? With the first expression there are six
different ways, but with the second expression there is only one
way. The required a's in the second expression must be the first
two a's of the string.
Two regular expressions are equal if they generate the same set of
strings. Here are some more regular expressions for the language
of strings containing at least two a's: (a+b)*ab*ab* and
b*a(a+b)*ab*. In the first one the required a's are the last two
a's of the string and in the second one the required a's are the
first and the last.
How would we write a regular expression for strings containing
exactly two a's? b*ab*ab*
How about at least one a and at least one b? Note that whatever
regular expression we choose must be able to generate both ab and ba.
Some expressions that do the job:
- (a+b)*a(a+b)*b(a+b)* + (a+b)*b(a+b)*a(a+b)*
- (a+b)*a(a+b)*b(a+b)* + bb*aa*
Here are some expressions that are equivalent to (a+b)*:
- (a+b)* + (a+b)*
- (a+b)*(a+b)*
- (a*b*)*
- (a*+b*)*
- a(a+b)* + b(a+b)* +
- (a+b)*ab(a+b)* + b*a*
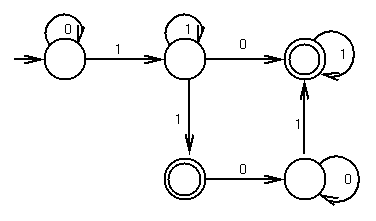
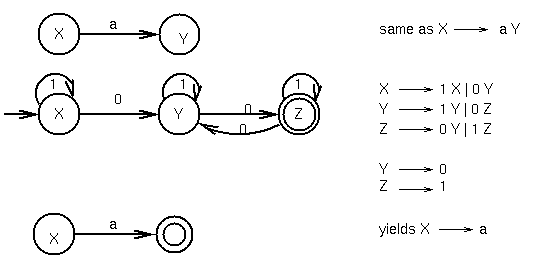
Regular expressions, regular grammars and FSA's
Theorem: Regular expressions, regular grammars and FSA's are all
equivalent---they can be used to define the same set of languages
The proof is ``constructive.'' That is given either a grammar G
or a FSA M, you can construct the other.
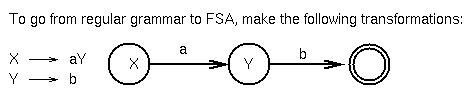
To go from a FSA to a regular grammar, make the following
transformations:
Why do we care about regular languages?
Programs are composed of tokens:
- Identifier
- Number
- Keyword
- Special symbols
Each of these can be defined by regular grammars:
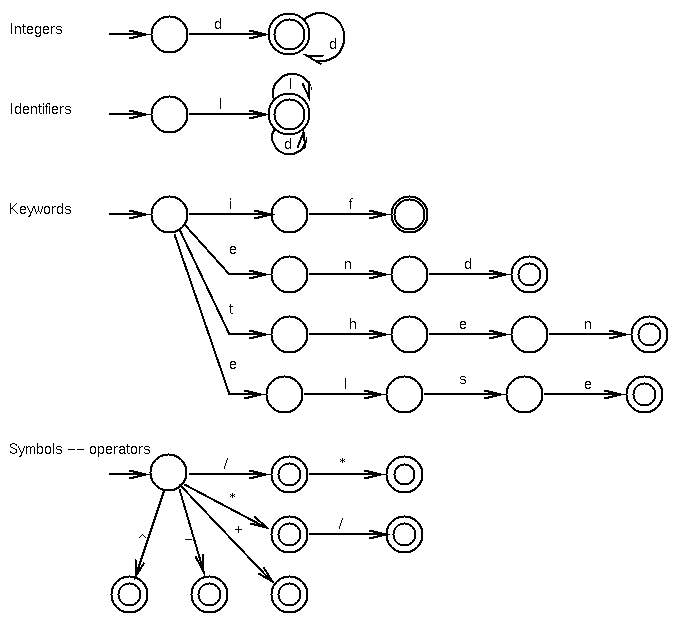
Examples
- Example 1: An even number of 0's and an
even number of 1's
- Example 2: a(bb)*bc
- Example 3: Binary Odd Numbers
- Example 4: 00(1|0)*11
- Example 5: Even Number of b's
- Example 6: At Most Two Consecutive b
Pushdown Automata (PDA)
Now let's look at a machine that
accepts context-free languages, the pushdown automaton or PDA.
This machine is fed input just as a finite automaton is. The input
tape is infinitely long in the rightward direction, which allows a PDA
to accept a finite input of any length. In addition to the input
tape, a PDA has an associated stack onto which it can push characters
to remember them. This stack has no limit to its size so the PDA can
push as many characters as it likes. The machine begins processing
with an empty stack.
Typically the first thing the machine does is push a
"bottom-of-the-stack marker" onto the stack.
We shall use the  as that marker. Note that a PDA has two associated alphabets,
one containing characters that may appear on the input tape, the
other containing characters that may be pushed onto the stack. The two
alphabets may be the same but they do not have to be.
as that marker. Note that a PDA has two associated alphabets,
one containing characters that may appear on the input tape, the
other containing characters that may be pushed onto the stack. The two
alphabets may be the same but they do not have to be.
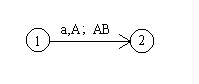
We will draw PDAs much like finite automata, except for the transition
labels. Each label will consist of three parts:
the input character, the character popped off of the top of the
stack, and the characters that need to be pushed onto the stack.
For example, suppose we find the following transition in a PDA:
We may use a 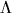 in any of the three parts of the
transition label. It always means that we do not do the task that
part of the label involves.
in any of the three parts of the
transition label. It always means that we do not do the task that
part of the label involves.
Here is a machine that accepts the language
{anbn | n 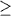 0 }.
The machine begins with its input on the input tape and an empty
stack. If the input was a correctly formatted string, the machine
will read a blank off the input tape at the same time that it pops
a blank off the stack and go to state 3 which is an accept state.
0 }.
The machine begins with its input on the input tape and an empty
stack. If the input was a correctly formatted string, the machine
will read a blank off the input tape at the same time that it pops
a blank off the stack and go to state 3 which is an accept state.
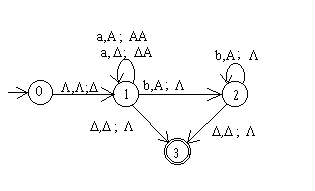
The previous machine shows that PDAs have more power than FSAs
because that machine accepts a nonregular language, something that
an FSA cannot do.
A deterministic PDA is one in which every input string has
a unique path through the machine. A nondeterministic PDA
is one in which we may have to choose among several paths for an
input string. We say that an input string is accepted if there is
at least one path that leads to an accept state. We shall see that
a nondeterministic PDA (NPDA)
is more powerful than a deterministic one (DPDA),
unlike the situation with FSAs and NFSAs.
Here is a PDA that accepts the PALINDROM language over the
alphabet {a,b,x}. PALINDROM =
{sxsR} where s is a string over {a,b} and sR
is the reverse of s.
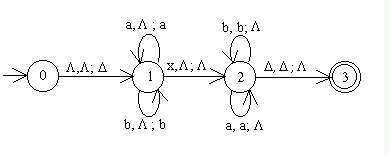
Note that there is only one path through the machine for
any string, although there is an implied trap state in the machine
and a string's path may take it to that implied trap state.
The x in the strings of PALINDROM is essential to our ability
to recognize the language with a deterministic machine. Without
the x we wouldn't know when to change states. Consider the language
PALINDROME2 which contains all odd length palindromes over {a,b}.
By changing the label (x,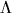 ;
;
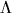 )
to the two labels (a,
)
to the two labels (a,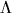 ;
;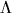 )
and (b,
)
and (b,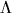 ;
;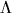 ),
we have an NPDA that recognizes PALINDROME2.
),
we have an NPDA that recognizes PALINDROME2.
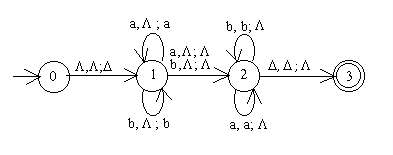
This machine is nondeterministic because from state 1,
when there is an a in the input, the machine can either stay in
state 1 and not pop the stack or it can go to state 2
and not pop the stack. Similarly, the machine has two choices if
it reads a b and it is in state 1.
Turing Machines
We already know that type 0 languages can be recognised by Turing
Machines. Turing machines may also be used as computational devices with
greater power than Push Down Automaton and Finite State Automaton.
How powerful are TM's
Alan Turing posited:-
Turings thesis: Each function for which
there is a rule to compute its value is a computable problem.
or
"Any well defined infiormation processing task can be carried out
by some Turing machine." (Parkes)
or
"Any computation that can be realised as an effective procedure can
also be realised by a Turing machine"
Definition: An effective procedure is a set of rules which tell
us, from moment to moment, precisely how to behave. (Minsky 1972)
This cannot be proved! However no cases disproving it have yet
been found. The existence of insoluble problems can be proved.
Any effective procedure must be stated in some language. This
can then be interpreted by some machine.
Definition
A Turing Machine (TM) consists of the following three components:
- A Finite State Machine
- A read/write head which can read or write symbols cells marked on a
tape.The head can also move the tape left or right or keep it in the same
position.
- An infinite tape, extending on either side of the read/ write head.
The FSM part of the TM must always be in one of a finite set of states
- S
The symbols read from and written to the tape are drawn from the external
alphabet - I
The direction of tape movement after an operation is drawn from
the set D = { L, R, N }
N is some times represented by hyphen -
Operation
The machine operates by:
- reading a symbol from the tape
- changing to a new state depending on the symbol read and the current
state
- writing a new symbol to the tape depending on the symbol read and the
current state
- moving the tape one cell left, one cell right or not at all.
A simple example
We can describe a TM by defining the external alphabet and three
functions.
- A machine function (MAF) which tells us what symbol to output.
- A state transfer function (STF) which tells us what state to move into.
- A direction function (MDF) which tells us which way to move the
tape.
This machine is a simple parity checker, it scans the tape from left
to right until it meets a 'B' symbol, it then outputs a '1' if an odd number
of 1's has passed under the head and 0 if an even number of
1's were scanned.
Alphabet I = { 1, 0, B } - these are the only symbols permitted on the
tape. It is conventional to assume that the rest of the tape is full of
0's.
|
MAF
|
|
|
|
X
|
Y
|
|
0
|
0
|
0
|
|
1
|
0
|
0
|
|
B
|
0
|
1
|
|
|
STF
|
|
|
|
X
|
Y
|
|
0
|
X
|
Y
|
|
1
|
Y
|
X
|
|
B
|
H
|
H
|
|
|
MDF
|
|
|
|
X
|
Y
|
|
0
|
R
|
R
|
|
1
|
R
|
R
|
|
B
|
-
|
-
|
|
This could be written more simply as
|
TM
|
|
|
|
X
|
Y
|
|
0
|
0XR
|
0YR
|
|
1
|
0YR
|
0XR
|
|
B
|
0H
|
1H
|
Alternatively as a State Transition Diagram.
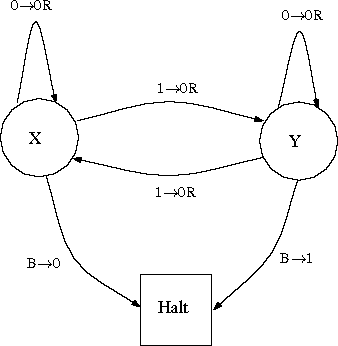
You will notice that this TM only moves its tape to the right. A TM
which only moves its tape in one direction is equivalent in computational
power to a FSM.
Try the tapes ...101101B...
^
and
The Universal TM
It is tedious to develop new turing machines for each new problem. It
would be very convenient if there was a single Turing machine which is
capable of performing all the computations possible for every other possible
Turing machine.
It may seem difficult to believe but this is perfectly possible. We
will not look at the solution in detail here but in principle we:
- Construct a notation for representing a Turing machine on a tape
- Construct a machine which can read this description and behave as if
it is executing it.
Coding TM's
In order to do this we need to code up a TM to go onto the tape.
We represent them as sets of quintuples.
(Current state, Input Symbol, Output Symbol, New State, Tape
Direction)
The quintuples for our parity checker are:
(X,0,0,X,R)
(X,1,0,Y,R)
(X,B,0,H,-)
(Y,0,0,Y,R)
(Y,1,0,X,R)
(Y,B,1,H,-)
We could use binary to code up these values e.g.
X as 00
Y as 01
H as 10
R as 01
L as 10
- as 00
0 as 00
1 as 01
B as 11
The quintuples are now
00 00 00 00 01
00 01 00 01 01
00 11 00 10 00
01 00 00 01 01
01 01 00 00 01
01 11 01 10 00
Ready to go onto a TM tape for a machine with only two symbols in its
alphabet. In practice to simplify the machine we would use a few more symbols
e.g. A Universal TM can be constructed with an alphabet of six symbols
and with 21 states. (Minsky again).
Some interesting points about Turing Machines
- Any Turing machine can be replaced by an equivalent machine which uses
only two symbols. This is remarkably convenient.
- A Turing machine with any number of extra tapes can be modelled by
one with a single tape.
- Any Turing machine can be replaced by an equivalent machine which uses
only two internal states.
Many other computational models have been proposed. It turns out that
is they can compute effective procedures they are exactly equivalent in
power to Turing machines.
An Incomputable Problem.
Can we design a Turing machine X which will accept as input a description
of another Turing machine Y and its input data D and halt after performing
some computation which will tell us if Y will halt when given D as
input data.
The answer is NO.
The proof is too complex to go into here but we can go through a proof
of a restatement of the problem by Goldschlager and Lister.
The Problem:
We want to know if a program P will halt when it is given some data
D.
We start by constructing a program halttester which given P and
D outputs "BAD" if P(D) does not halt and "OK"
if P(D) does halt.
A simpler version of this newhalttester tests a program that
takes itself as input and outputs "BAD" if P(P) does
not halt and "OK" if P(P) does halt.
Now we build a program funny :
Now we execute funny(funny)
This means:
- If funny stops when applied to itself then it willl loop forever
- If funny loops forever then it will stop when applied to itself
How can we resolve this?
There must be a flaw in the above argument.
The only flaw in the above argument is believing that halttester can
be written it is the only assumption in the whole argument.
Fun With Formal Models
Check out this web site
Complexity
Computations can be characterised by the length of time taken to complete
them. This is generally expressed in terms of the number of items of data
which need to be processed. The following table shows how long computations
would take on a computer capable of performing 1 million operations per
second.
n
(no. of data) |
k |
n |
nlogn |
n2 |
n3 |
2n |
|
10
|
1S |
10 |
10 |
100 |
1mS |
1mS |
|
20
|
1S |
20 |
26 |
400 |
8mS |
1.05S |
|
30
|
1S |
30 |
44 |
900 |
27mS |
17.9min |
|
40
|
1S |
40 |
64 |
1.6mS |
64mS |
127days |
|
50
|
1S |
50 |
85 |
2.5mS |
125mS |
35.7years |
|
60
|
1S |
60 |
107 |
3.6mS |
0.21S |
36,558years |
|
70
|
1S |
70 |
129 |
4.9mS |
0.34S |
37million years |
|
80
|
1S |
80 |
152 |
6.4mS |
0.5S |
38 billionyears |
|
90
|
1S |
90 |
176 |
8.1mS |
0.7S |
2 x 1012 years |
|
100
|
1S |
100 |
200 |
10mS |
1S |
4 x 1016 years |
|
1000
|
1S |
1mS |
3mS |
1S |
2.8min |
3 x 10287 years |
Computations often occur in typical patterns. e.g.
A calculation which,
- does something to each data item in turn takes time proprtional to
the number of items n
- does the same thing regardless of input data, takes a constant time
- for each item of data, does something to all the other items takes
time proportional to n2
- for each item of data does something to all the items of data that
have not yet been processed)
e.g. for i = 1 to n do
for
j = i to n do
do
something
take time proportional to n2/2
- tries every possible combination of input data takes time proportional
to 2n
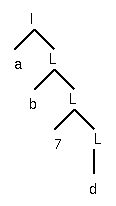






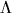



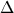 as that marker. Note that a PDA has two associated alphabets,
one containing characters that may appear on the input tape, the
other containing characters that may be pushed onto the stack. The two
alphabets may be the same but they do not have to be.
as that marker. Note that a PDA has two associated alphabets,
one containing characters that may appear on the input tape, the
other containing characters that may be pushed onto the stack. The two
alphabets may be the same but they do not have to be.

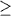 0 }.
The machine begins with its input on the input tape and an empty
stack. If the input was a correctly formatted string, the machine
will read a blank off the input tape at the same time that it pops
a blank off the stack and go to state 3 which is an accept state.
0 }.
The machine begins with its input on the input tape and an empty
stack. If the input was a correctly formatted string, the machine
will read a blank off the input tape at the same time that it pops
a blank off the stack and go to state 3 which is an accept state.



