home | homework index | labs index
|
|
CSCI 201
Introduction to Algorithm Design home | homework index | labs index |
SPRING 2007 |
This lab will introduce you to how Java programs work with numbers and expressions.
As you should know from your reading, numbers in Java come in six different categories which differ in range and precision. But just in can you can't remember the details, here's a little table to help you out.
| Type | What it Holds |
|---|---|
| byte | Holds a whole number from -128 to 127. |
| short | Holds a whole number from -32,768 to 32,767. |
| int | Holds a whole number from -2,147,483,648 to 2,147,483,647. |
| long | Holds an whole integer from -9,223,372,036,854,775,808 to 9,223,372,036,854,775,807. |
| float | Holds a decimal number with a range of about -1038 to 1038 and a precision of about seven decimal digits. |
| double | Holds a decimal number with a range of about -10308 to 10308 and a precision of about fifteen decimal digits. |
In the table below, you see four range testers written as a Java applet. The five buttons for these applets can be used to modify the displayed numbers. For example, when you press the * 10 button, the number is multiplied by 10. The number is stored in six different ways. Originally all six numbers are the same, but with additions and multiplications the numbers will start to differ.
Below each tester is a short little exercise we'd like you to try out. Read the description with each exercise to increase your understanding of the limitations of computer arithmetic.
Try to set this number to 1000 (103).
Notice that the
byte
has already exceeded its maximum capacity. It is now displaying a negative
number very different from 1000. |
|
Try to set this one to 1000000050 (109+50).
Notice that the
byte
and short have been long exhausted. However, there's
something interesting about the float. Although a
float can hold a number as large as 1038,
it can only hold seven significant decimal places. So, it
can't distinguish between 1000000000 and 1000000050. |
|
Try to set this one to 1000000000000000050 (1018+50).
This number is near the top of the range for a
long.
Notice that the double can't hold this precise value. |
|
Patiently go up 1040. Everything but the
double
is in trouble. The float even holds a special value
corresponding to positive infinity. |
|
Show the instructor your numbers.
Programmers need to understand a bit about how different data types are stored in the computer. Here we are going to look at how integers are stored in the computer. We've written a Java applet to give you a little practice in converting decimal numbers to their binary representations.
In the table below, you'll see some decimal numbers in the left hand side. These are your targets. In the middle of the table, you see a row of black and red dots. These represent bits or binary numbers. Red means binary 1. Black means binary 0. Go ahead and mash one of the dots. It changes state -- 0 becomes 1, 1 becomes 0. Notice that the rightmost number also changes. It is the decimal number corresponding to the binary number.
Your job is to set the binary bits so that the right column matches the left column, if possible. This can be a little tricky for negative numbers as they are encoded in twos complement notation as required by the Java virtual machine specification. In this case, first find the positive number number that is one less than the absolute value of the negative number and then reverse all the bits. For example, if the goal is to find -127, first find 126 and then reverse all the bits.
To convert decimal to binary
There are several ways to convert decimal numbers into binary. It can be achieved by repeated division by two, and recording the remainder each time.
Starting with decimal number 90:
90 / 2 = 45 remainder 0
45 / 2 = 22 remainder 1
22 / 2 = 11 remainder 0
11 / 2 = 5 remainder 1
5 / 2 = 2 remainder 1
2 / 2 = 1 remainder 0
1 / 2 = 0 remainder 1
The binary equivalent reads from the bottom up, so 90 (decimal) = 1011010 (binary).
Twos Complement Notation
To change the sign of signed binary integer you will need to convert 0 bits to 1 bits and 1 bits to 0 bits, then add 1 to the result.
Example:
0000000001011010 (+90 decimal) 1111111110100101 + 1 = 1111111110100110 (-90 decimal)10100110 (-90 decimal)
Start off with eight bit numbers. These correspond to the
Java byte type.
| Target | Your guess |
|---|---|
| 20 | |
| 43 | |
| 66 | |
| 99 | |
| 127 | |
| 128 |
Now try out binary representations using 16 bits.
These correspond to Java short integers.
| Target | Your guess |
|---|---|
| 128 | |
| 201 | |
| -201 | |
| 32767 | |
| -32768 | |
| -1 |
Ask your lab instructor to verify that you've pushed all the right buttons.
But what about floating point? Well, that's harder. Below you see the bits of 2006 as a floating point number. The three fields of the number are: (1), sign, in light red; (2), exponent, in light green; and (3), fraction, in light blue. If you press the left-most button in the display, you change the sign of the number. If you press the right-most button, which is the last bit of the fraction, you make a tiny change to the number. If you press buttons toward the left end of the fraction (blue) zone, you'll see larger changes. If you press buttons in the exponent (green) zone, there will be some big changes.
If you are adventurous, you can try to find the two button presses that change 2006 to 1492.
Java executes expressions according to the order of operations you learned in high school algebra. We hope you know this by heart, but if you've forgotten, just remember that expressions inside of parenthesis are evaluated first, and that the operators multiplication, division and remainder are evaluated before the operators addition and subtraction.
An expression contains operators that must be evaluated.
Usually expressions appear in assignment statements of the form:
Variable = Expression
In such statements, the expression is
evaluated and the result of the evaluation is then
assigned to the variable. This process is illustrated in the
following Stack N' Heap simulation:
Begin by using the following link to download a ZIP file called Expr.zip. Then extract the directory Expr into your csci/201 directory.
Next start up NetBeans and open the project you now have stored in your csci/201/Expr directory.
If you do not remember how to do this, you may go back to the downloading projects lab. Your lab instructor may be willing to help you with the extraction this week, but by next week this activity needs to be on auto-pilot.
You must make your Projects panel look
something like the following picture before continuing. If you are having
trouble obtaining this layout, call your instructor (or a fellow student) now.
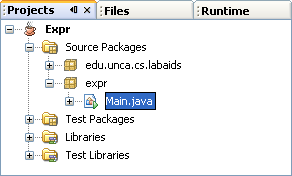
Study, build, and run the Main class of the
expr package.
Presently, this program uses a random number generator
(edu.unca.cs.labaids.TestValues)
to generate four numbers, two integers i
and j
and two double-precision floating point numbers
y and z,
and then displays the result of evaluating
expression 1 in the table below.
Your job is to modify the main method to print
all of the
ten expressions listed in the table below.
Notice that the first expression is already done for you. When you run your
program it will display results of your code as well as correct answers.
To verify if you answers are correct, you should copy the "solution set" number is displayed by your running program and type it into the Solution Set Number field of the Java applet running below on the right.
| Expression Number |
Expression | |
|---|---|---|
| 1 | Average of y and z |
|
| 2 | Average of i and j
as a decimal number |
|
| 3 | The remainder when i is
divided by j |
|
| 4 | y2 +
4 j z |
|
| 5 | -(y2 - z3) |
|
| 6 | (y + z)
/ (y - z) |
|
| 7 | i / (i + 1) |
|
| 8 | i / (i + 1.0) |
|
| 9 | (i / j) * j |
|
| 10 | iy
Hint: Use the pow method of the Math class.
|
After you have thoroughly tested your code, and you understand why the expressions print as they do, ask your instructor to test your code.
Last modified: 02/08/07