Solution CSCI 311 / ENGR 212 / ECE 212 Homework Assignment 7

Problem 1

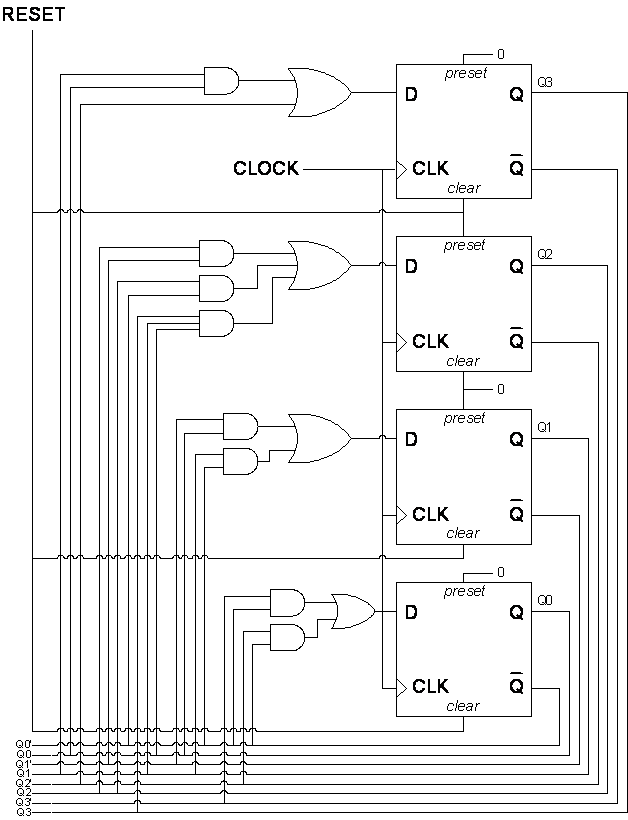
Write a VHDL behavioural specification for the majority function. Assume the input variables are X, Y, and Z and the output variable is M.

The answer should be a single line similar to:

• A <= (X and Y) or (not X and not Y) ;

• M <= (X and Y) or (X and Z) or (Y and Z) ;

Problem 2

Problem 2(a)

Design a 4-bit binary counter that counts modulo-9 with the counting sequence:

• 4, 5, 6, ..., 12, 4, 5, ...

Design this as a custom circuit using gates and flip-flops. That is, begin with a state table and synthesize the circuit from the state table. Exploit don't-care states if applicable. Use an external asynchronous RESET input to initialize the flip-flops to the initial state.

Problem 2(b)

Repeat subproblem 2(a), but use a 74x163 as the basic building block, and add external logic to drive the counting sequence. Use an external synchronous input called init for initializing the counting sequence.

Problem 2(c)

Which approach was easier? Which approach was less expensive? Explain your answer.

Approach (b) was certainly easier. It is also less expensive if the number of discrete chips and external wires determines the cost/size of the system. Part (a) requires two 7474 D flip-flop chips (four D flip-flops), and at least several 2-input/3-input NAND chips (convert AND-OR logic to NAND-NAND logic). Part (b) requires one 74x163 chip and one or two other chips (depending on exact implementation of the external logic… can map the logic onto a NAND chip). Another cost factor is the time needed to design a circuit: engineering effort. Approach (b) is certainly less costly in terms of engineer-hours.

Problem 3

Problem 3(a)

Design a Mealy state machine to detect the sequence 10010. There is a single input x and a single output z. The output is set to 1 when the sequence is detected

Design the state machine using gates and flip-flops in the standard way, i.e., begin with a state diagram and state table, do plain state assignment (e.g., for three state variables, first state is 000, next is 001, and so on), use K-maps to derive minimized next-state and output equations (exploit don't-care states if applicable), and synthesize the circuit diagram from the equations.

Problem 3(b)

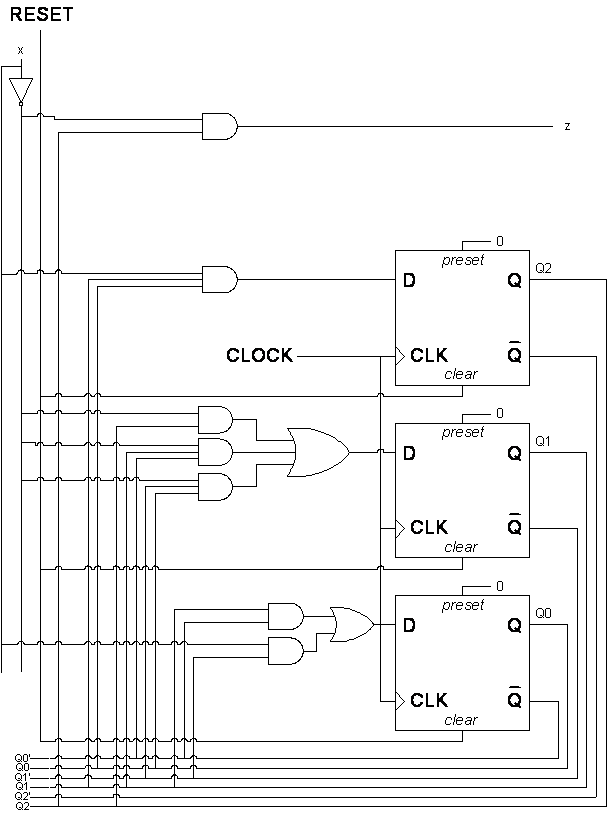
Repeat problem 3(a), but this time use a shift register to design your circuit.

Problem 3(c)

Which approach was easier? Which approach was less expensive? Explain your answer.

Approach (b) was certainly easier. It is also less costly and takes less space, in terms of discrete chips and external wires. The shift register design probably requires 3 chips: 2 7474 D flip-flop chips (four D flip-flops) and 1 3-input AND chip (two AND gates can form the 5-input AND logic), assuming complemented outputs of flip-flops are used instead of inverters at inputs of AND logic. The non-shift-register design would also use 2 7474 D flip-flop chips (5 states encoded with 3 flip-flops), plus several chips for next-state and output logic. Another cost factor is the time needed to design a circuit, the engineering effort. Approach (b) is certainly less costly in terms of engineer-hours.

Problem 4

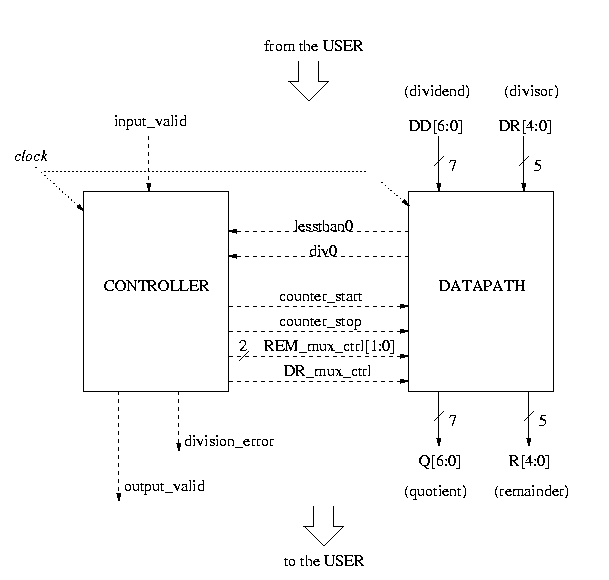
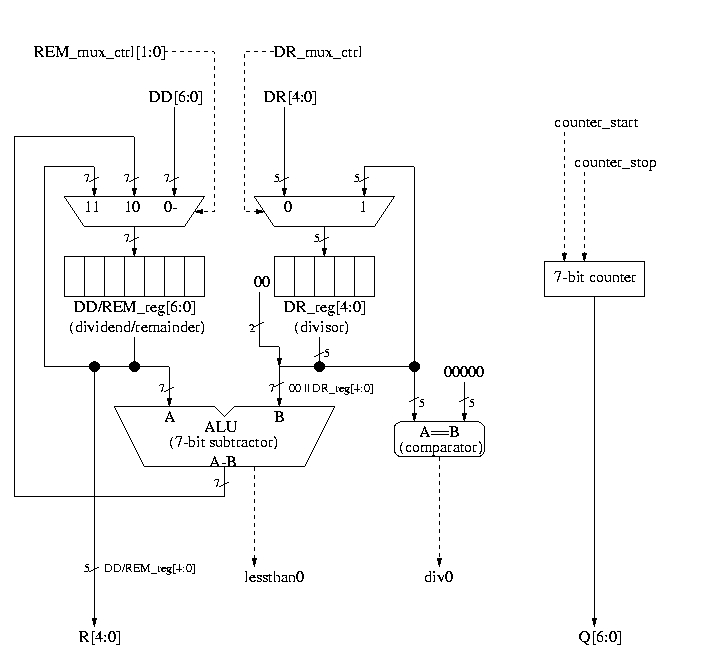
Design a division circuit that will divide a 7-bit number by a 5-bit number. You'll do the division by successive subtraction, continually subtracting the 5-bit number from the 7-bit number until no further subtractions are possible. You'll then report the quotient and remainder of the operation.

• Inputs:
  • 7-bit unsigned integer, presented as DD_6:0
  • 5-bit unsigned integer, presented as DR_4:0
  • Input_Valid, a control signal present when the DD_6:0 and DR_4:0 values are valid. Input_Valid will remain active for one clock period. This signal should be used to initiate the division process. You may assume that Input_Valid is never asserted while another division is underway, only when the machine is idle.
  • Clock, used for clocking all flip-flops.
• Output
  • 7-bit quotient, Q_6:0
  • 5-bit remainder, R_4:0
  • Division_Error, to signal that an error has occurred (i.e., divide by zero).
  • Output_Valid, a signal that indicates that the quotient and remainder values are valid, or that the Division_Error signal is set. You only need to assert output_valid for one cycle.
• Suggested internal organization:
  • Registers to latch the dividend (DD_6:0) and divisor (DR_4:0) when the Input_Valid signal appears.
  • Counter, which will serve as the quotient (Q_6:0), by counting the number of successful subtractions.
  • An ALU that will do the successive subtractions. You may assume the ALU is already configured to perform unsigned 7-bit subtraction. The ALU also indicates when the result of a subtraction is less-than-0.
  • You will need to use other components, e.g., MUXs and comparators.

Your design should include the datapath unit and the control unit of the system and the signals that interact between them. Your final design should show:

1. A top-level diagram of the overall system showing
   • inputs tothe overall system
   • outputs from the overall system, and
   • control signals and condition signals between the datapath unit and control unit.
2. A block diagram of the . Elements like ALUs, MUXs, comparators, registers, counters, etc., should be represented by an appropriate symbol and should not be shown at the level of individual gates.
3. The state diagram for the control unit. You do not have to synthesize a circuit for your state machine.

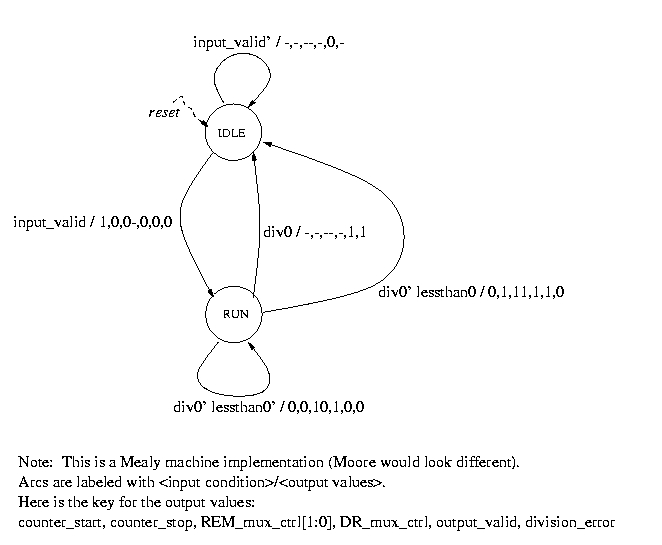
Different solutions are possible, because of slightly different datapaths, timing assumptions, Mealy vs. Moore implementation, and design style. But the fundamental aspects of the datapath should be the same. Here is one possible solution...

Top-level diagram of the overall system

Block diagram of the datapath

State diagram for the control unit