ECE 212-001: Homework Assignment #6
1. For the FSM (Finite State Machine) specified by the state table below,
x
--------------
state 0
1
---------------------
A A/1
B/1
B B/0
C/0
C A/0
D/1
D B/0
A/1
--------------
state* / z
(a) Draw the corresponding state transition diagram.

(b) Show the K-maps for the next-state (Q1* Q2*) and output (z).

(c) Derive the minimized next-state (Q1* Q2*) and output (z) equations by deriving their minimum sums.

(d) Derive the minimized next-state (Q1* Q2*) and output (z) equations by deriving their minimum products.

For (b)-(d), use the following state assignment for Q1 Q2:
A = 00, B = 10, C = 11, D = 01.
2. Using the state table in problem #1:
(a) Show the K-maps for the next-state (Q1* Q2*) and output (z).

(b) Derive the minimized next-state (Q1* Q2*) and output (z) equations by deriving their minimum sums.

For (a)-(b), use the following state assignment for Q1 Q2:
A = 11, B = 10, C = 00, D = 01.
(c) Compare your solutions for problems #1 and #2, which one is simpler? How does state assignment affect your solution?
Note that both solutions use all literals and their complements (x, x’, Q1, Q1’, Q2, Q2’).
|
|
unique product terms |
Number of |
Number of |
Number of |
Number of |
|
solution from problem #1 |
Q1 Q2’ x Q2’ x’Q1’Q2 x Q1 Q1’Q2’ x Q2 |
5 |
1 |
1 (for z) |
1 (for Q1*) |
|
solution from problem #2 |
x’ Q2 Q1’Q2’ x Q1’ x’Q1 Q2 Q1 Q2 |
3 |
1 |
2 (for Q1*, z) |
1 (for Q2*) |
The solution from problem #2 is simpler. It uses a total of 7 gates whereas the previous solution uses 8. This was made possible by the fact that the x Q1’ term appears twice (for Q2* and z) and is therefore reusable (saves one AND gate). Moreover, the solution from problem #2 uses the same number of 3-input gates (1 3-input AND, 1 3-input OR), so it is not worse in that respect. We conclude that state assignment can affect overall complexity of the final circuit, therefore, the designer should attempt to find the best state assignment, after designing the state machine and before synthesizing the circuit.
3. For the FSM (Finite State Machine) specified by the state table below,
x1 x2
--------------
state 00
01 10 11
z1 z2
--------------------------------
A D
A D A 0 1
B B B A
C 0 1
C C A
C B 1 0
D D D A A 1 0
-------------
state*
(a) Draw the corresponding state transition diagram.
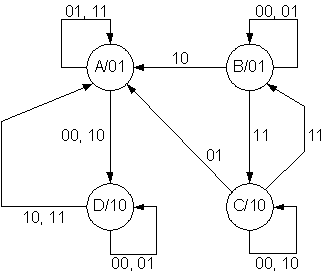
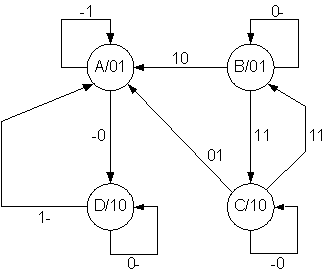
Here is an alternate diagram – it is functionally equivalent but the arcs are labeled in a more compact form (e.g., 01, 11 can be combined into -1, meaning x1 can take on either 0 or 1).
(b) Show the K-maps for the next-state (Q1* Q2*) and outputs (z1, z2).
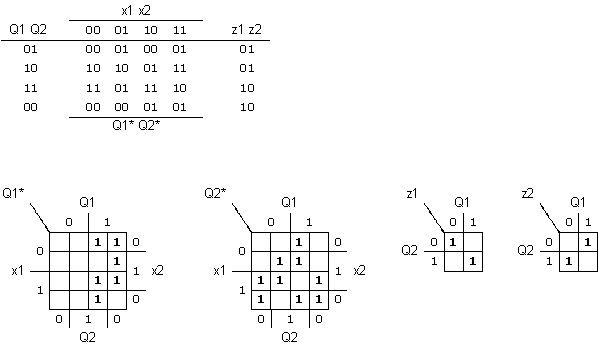
(c) Derive the minimized next-state (Q1* Q2*) and output (z1, z2) equations by deriving their minimum sums.

For (b) and (c), use the following state assignment for Q1 Q2:
A = 01, B = 10, C = 11, D = 00.
4. Using the state table from problem #1, construct a state sequence chart for the input sequence:
x = 0 1 1 0 1 1 0 0 0 1.
The initial state is "A".
Note: A state sequence chart shows input, current state, next state, and output each cycle. For example, here is the first cycle done for you:
cycle 1 2 3
4 5 6 7 8 9 10
------------------------------------
x (input) 0 1 1 0 1 1 0 0
0 1
current state A A B C A B C A A A
next state A B C
A B C A A A B
z (output) 1 1 0 0 1 0 0
1 1 1
5. Design a Mealy state machine that will detect each of the following sequences. When the sequence is detected, a single output "z" is set to 1. Your design should include a state diagram and a state table for each machine.
(a) Sequence = 10010

x
--------------
state 0
1
---------------------
A A/0
B/0
B C/0
B/0
C D/0
B/0
D A/0
E/0
E C/1
B/0
--------------
state* / z
(b) Sequence = 0101

x
--------------
state 0
1
---------------------
A B/0
A/0
B B/0
C/0
C D/0
A/0
D B/0
C/1
--------------
state* / z
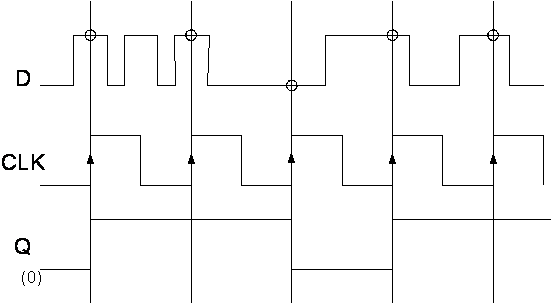
6. Suppose the waveforms below are applied to the D and CLK inputs of a positive edge-triggered D flip-flop. Draw the waveform for Q, the output of the D flip-flop. PRINT THIS PAGE, DRAW YOUR WAVEFORM ON IT, AND HAND IT IN WITH YOUR HOMEWORK.
(Note: The initial state of Q is 0.)
(Note: Assume zero propagation delay when drawing your waveform.)