Spring 2003 ENGR 212 Homework 2

This homework is due 5 February, 4:30 PM.

Problem 1

For each of the three equations show below do the following actions:

• Draw the logic circuit diagram that directly implements the function. That is, OR and AND gates should match sum and product terms in the original equation.
• Construct the truth table.
• From the truth table, rewrite the equation in canonical sum-of-products (SOP) form, and then use shorthand SOP notation.
• From the truth table, rewrite the equation in canonical product-of-sums (POS) form, and then use shorthand POS notation.
• Draw the logic circuit diagrams for the Boolean expressions below using only two-input or three-input NAND gates.

1. f(a, b, c) = (a + b' + c')(a + c)
2. f(x, y, z) = (x(y + z'))'
3. f(a, b, c) = (a ⊕ b') + a c'

Note: ⊕ is the "exclusive-OR" function.

Problem 2

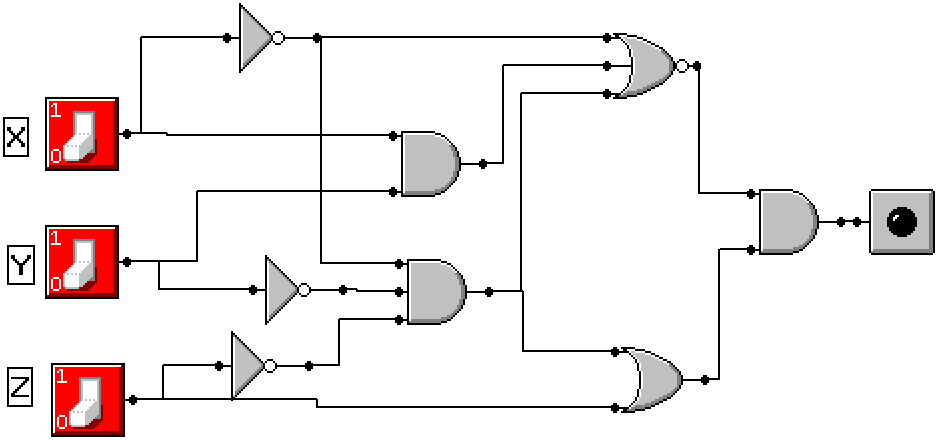
Do the following for the circuit drawn below:

• Derive the Boolean equation corresponding to the circuit. Do not simplify the expression! Sum and product terms should exactly match OR and AND gates in the circuit diagram.
• Simplify the Boolean equation using only switching algebra theorems. Show all of your simplification steps! Express the simplified equation in sum-of-product form.
• How many AND gates and OR gates are needed to implement your simplified expression?
• Derive the sum-of-product Boolean equation that produces the exact opposite (complement) of the circuit drawn below.

Problem 3

A control panel for a rudimentary robot has three Control switches and one Power switch. Each switch has two positions -- ON or OFF. The control switches are labeled x , y, and z. The Power switch is labeled p. In order for the robot to be Enabled), the Power switch must be ON, and exactly two of the Control switches must ON. Design the logic circuit to generate the Enable signal. Show your results with a truth table, Boolean (algebraic) expression, and the logic circuit diagram.

Problem 4

Simplify the following expressions using only boolean algebra. Show all your steps for credit.

1. F(x, y, z) = x + x' y + z
2. F(x, y, z) = x + y + x z + (x y z)'
3. F(x, y, z) = (x + y)(x' + z)(y + z')
4. F(x, y, z) = ((((x + y)' + z)' + x)' + y')'
5. F(x, y, z) = x (y + z(x + y z') + x' z') x'
6. F(x, y, z) = x + x' z + x' z'