Spring 2001 CSCI 255 Homework 2

You must show your work to receive full credit. This assignment is due Monday, 5 February.

Problem 1

Add the following six-bit twos-complement number. Which, if any, of the additions result in an overflow?

111000 + 101010
010111 + 001111

Problem 2

Compute the following bit-wise logical operations on six-bit binary numbers.

011011 AND (101000 OR 000001)
NOT(001100) AND NOT(011110)

Problem 3

Translate the first four characters of your last name into an ASCII hexadecimal string.

Problem 4

The following 32-bit strings represent IEEE floating point numbers. Translate the bits into their "normal" floating point representation. This is not an easy problem.

01000001001010000000000000000000
11000100110000000000000000000000

Problem 5

Draw a circuit that implements the truth table shown below. The "inputs" to the truth table are A, B, and C. The output is Z. Review section 3.3.4 before attempting this problem.

input			output
A	B	C	Z
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

Problem 6

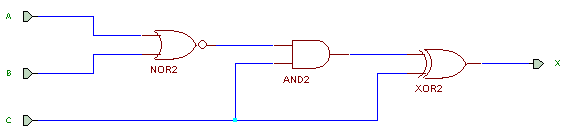
Complete a truth table to describe the logic circuit shown below.
Problem 6 logic circuit