The problem is to design a Nabs dispenser. The Nabs machine has two inputs, x and y, which encode the following information:
| x | y | Meaning |
|---|---|---|
| 0 | 0 | nothing is happening |
| 0 | 1 | nickel inserted |
| 0 | 1 | dime inserted |
| 1 | 1 | Nabs button pushed |
There is a single output, z. When z is 0, the machine produces nothing. When z is 1, the machine outputs a package of Nabs.
Assume that Nabs cost 15 cents. Nabs are returned only if the Nabs button is pushed after 15 cents are deposited. Assume that this %!@%$# machine returns no change and just keeps any money you deposit over 15 cents.
Draw the finite state machine for the Nabs dispenser below.
| x | y | A | B | z | A | B | jA | kA | jB | kB |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ? | 0 | ? |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | ? | ? | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | ? | 0 | 0 | ? |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | ? | 0 | ? | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | ? | 1 | ? |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | ? | ? | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | ? | 0 | 1 | ? |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | ? | 0 | ? | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | ? | 0 | ? |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | ? | ? | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | ? | 0 | 1 | ? |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | ? | 0 | ? | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ? | 0 | ? |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | ? | ? | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | ? | 0 | 0 | ? |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | ? | 1 | ? | 1 |
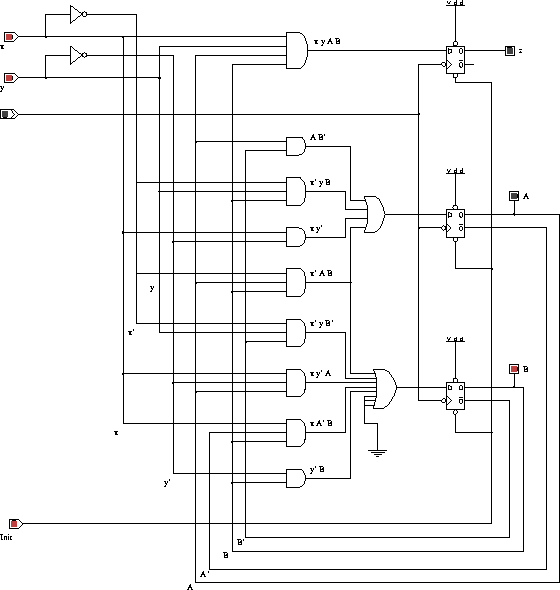
These Boolean functions were optimized by espresso. Two optimizations were performed: one for the implementation with D flip-flops and another for the implementation with JK flip-flops.
| z = Sigma(15) | |
| z = x y A B | |
| dA = Sigma(2, 3, 5, 6, 7, 8, 9, 10, 11, 14) | |
| dA = x' y B + A B' + x y' + x' A B | |
| dB = Sigma(1, 3, 4, 6, 7, 9, 10, 11,13) | |
| dB = x' y B' + x A' B + x y' A + x' A B + y' B | |
| jA = Sigma(5, 8, 9) | jA = d(2, 3, 6, 7, 10, 11, 14, 15) |
| jA = x' y A' B + x y' | |
| jB = Sigma(4, 6, 10) | |
| jB = d(1, 3, 5, 7, 9, 11, 13, 15) | |
| jB = x' y + x y' A | |
| kA = Sigma(15) | kA = d(0, 1, 4, 5, 8, 9, 12, 13) |
| kA = x y A B | |
| kB = Sigma(5, 15) | kB = d(0, 2, 4, 6, 8, 10, 12, 14) |
| kB = x' y A' B + x y A B | |
Press here to retrieve a copy.
Press here to retrieve a copy.
Return to CSCI 274 home page
Return to Dean Brock's
home page
Return to the UNCA Computer Science home page