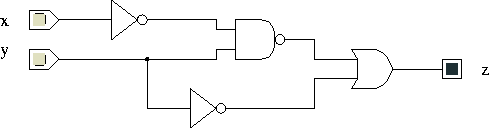
Express your answer by completing a truth table corresponding to the circuit.
This is an open book, open notes exam. It is to be turned in by 5:30 PM.
Use a truth table to show that the following two Boolean expressions are equivalent:
| x | y | your stuff goes here |
|---|---|---|
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
Simplify the following Boolean expression using Boolean algebra.
Simplify the following Boolean function using a Karnaugh map. Notice the "don't care" conditions. Be sure to write your answer as a minimal sum-of-products Boolean Function.
What would the espressoinput for the Boolean described in Problem 3 look like? (Start with the following.)
.i 3 .o 1 .ilb x y z .ob F # it's all yours from this point on
What is the Boolean function computed by the following circuit?

Express your answer by completing a truth table corresponding to
the circuit.
| x | y | z |
|---|---|---|
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 |
How should the Jand Kinputs of a JK flip-flop be set to make the output of the flip-flop change from 1 to 0 on the next clock cycle?
How should the J and K inputs of a JK flip-flop be set to make the output of the flip-flop be 1 on the next clock cycle regardless of the present output?