Vending machine example

The problem is to design a Nabs dispenser. The Nabs machine has two inputs, x and y, which encode the following information:

There is a single output, z. When z is 0, the machine produces nothing. When z is 1, the machine outputs a package of Nabs.

Assume that Nabs cost 15 cents. Nabs are returned only if the Nabs button is pushed after 15 cents are deposited. Assume that this %!@%$# machine returns no change and just keeps any money you deposit over 15 cents.

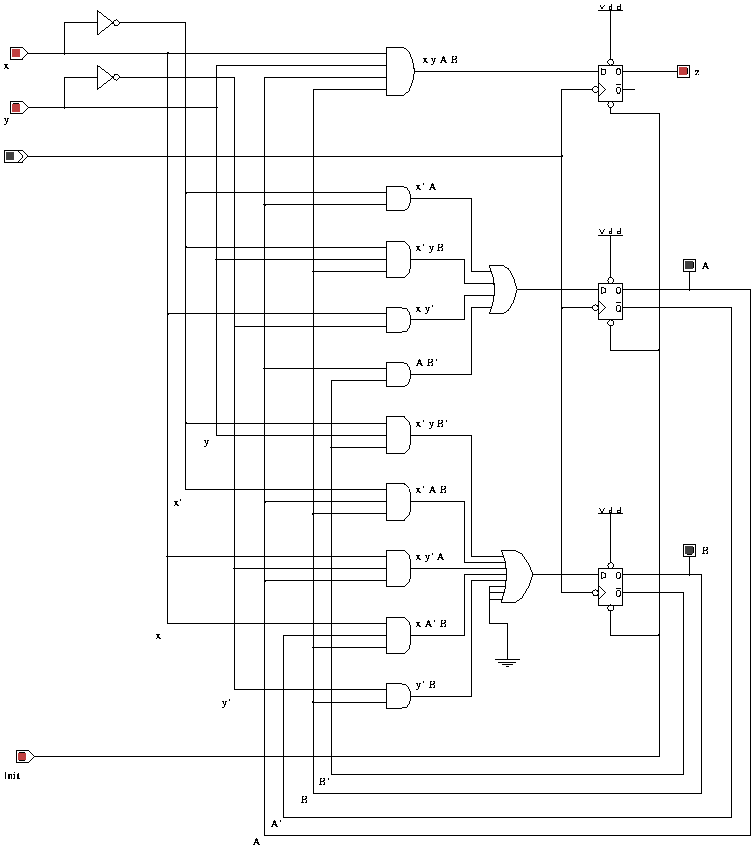
Draw the finite state machine for the Nabs dispenser below.

The state table

The Equations

• z = Sigma(15)
• z = x y A B

• DA = Sigma(2, 3, 5, 6, 7, 8, 9, 10, 11, 14)
• DA = x' A + x' y B + x y' + A B'

• DB = Sigma(1, 3, 4, 6, 7, 9, 10, 11,13)
• DB = x' y B' + x' A B + x y' A + x A' B + y' B

• JA = Sigma(5, 8, 9)
• JA = d(2, 3, 6, 7, 10, 11, 14, 15)
• JA = x y' + x' y B

• KA = Sigma(15)
• KA = d(0, 1, 4, 5, 8, 9, 12, 13)
• KA = x y B

• JB = Sigma(4, 6, 10)
• JB = d(1, 3, 5, 7, 9, 11, 13, 15)
• JB = x' y + x y' A

• KB = Sigma(5, 15)
• KB = d(0, 2, 4, 6, 8, 10, 12, 14)
• KB = x' y A' + x y A

Implementation with D flip-flops

Press here to retrieve a copy.

Implementation with JK flip-flops

Press here to retrieve a copy.

Back to the Handout index